Main Page


My Games

My Projects

My Music

My Art

My Literature
- Technical Articles
- | -
- | -
- | -
- Poems
- Definitions
- Quotes
- Language Problems
- Stories
- Documentation

Links

Particle Systems Overview


Particle systems can be used to create a very large range of effects. They are generally comprised of a large number of individual particles moving either along a parametric function, or as independent objects with their own simple physics. The individual particles themselves can be either 2D or 3D, and could be anything from a few scattered pixels to a fully rendered 3D model. The most common particle is a 2D sprite of some form (in 3D, it is billboarded towards the user).

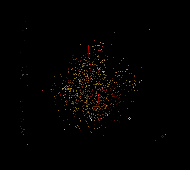
In most cases, a particle system has one or more emitters. These emitters are responsible for adding a new particle to the system on a regular interval. For example, if you had a particle system for showing smoke, a car in the world might have a particle emitter attached to it's tailpipe. Every fraction of a second a new smoke particle would be added to the system at the location of the tailpipe. This way if the car moves, it leaves a trail of smoke behind it. Another example of an effect like this is a missile leaving a smoke trail behind, as in the below image from Astrocosm (an old DirectDraw game I made that uses pixel-based particles):

The exact data fields stored in particles depends on what the desired effect is. Most particles have both a position and a velocity at a minimum. In the above example of the car, the initial velocity of the particles would be based on the direction the tailpipe is pointing. This would allow smoke to come out of the tail pipe and move away, even if the car is not moving. Another example would be an simple explosion. The initial velocity of these particles could just be random vectors in any direction with some random variation in their speed. This would make the particles move outward in a semi-irregular but circular fashion. For example, look at the following images from an explosion in Astrocosm:

explosion near start

    

explosion near end

Most particles have a limited lifespan, and also change as they grow older. As you can see in the above images, the particles have become more faint as they spread out. Also note that colors of the particles have changed from reddish-yellow towards more of a gray. Other common attributes that vary with life, are size and speed. As with most other attributes of particles, it's often best to vary the lifespan randomly a little bit. The only metaphor I can come up with for why randomly varying attributes can help particle systems look better, would be that it is sort of "dithering" the system.


Particle Interactions and Motion


Having particles that move in the world is a good start, but it can often seem unnatural for them to just move in straight lines. Adding a lot of complex calculations to particle movement can hurt the framerate badly though. One of the major things to balance when working on a particle system is complexity of particles vs number of particles. In most cases, you want to have a very large number of particles to make the system seem more continuous. There are a number of very simple things that can be applied to particle movement that can greatly improve how the system looks.

For many systems, the simplest addition is gravity. If your already storing the velocity for each particle, gravity also has the advantage in that it requires no additional memory. Since gravity is basically an acceleration, you can simply do the following (assuming positive z is up):
Velocity.z -= (GRAVITY_AMOUNT * time)
(where GRAVITY_AMOUNT is a constant that you can tweak, and time is the amount of time that has passed)
Similarly, a wind force is easy to apply. Simply use the same equation as above, replacing the z axis adjustment with an arbitrary vector that affects all components of the velocity. Here's an example of wind force being applied to a smoke particle system (from the demo below):

Another major type of particle interaction is collisions. Collisions with other particles is generally not preferable as the number of calculations grows proportional to n², which would severely limit the number of particles you could have. In some cases collisions with objects is feasible, but in many cases you can get by checking against one or more planes. If the plane your checking against is aligned with one of the axies, then you can do your collision check with a single if statement. The water portion of the demo below checks all particles against 3 parallel planes; the top two planes are circular in shape as shown below:

Constraining a plane to a circular section is relatively simple. After checking against collision with the plane, calculate the distance of the center of the particle to the center of the circular region (xy plane only, if z is up), then compare that to the radius of the circular region.

A common mistake with systems that continuously generate particles, is not compensating for irregularities in time. A naive implementation of an emitter might do something like this:
timeLeft -= timePassed;
if (timeLeft<0)
{
     timeLeft=1.0f/CREATION_FREQUENCY;
     CreateParticle();
}
 (where timeLeft is the time until the next particle creation)
The problem with this approach is if you ever drop below CREATION_FREQUENCY frames per second, then there will be noticeable gaps between particles. Even if you think your framerate will be perfectly smooth, you don't always know what else is running on the computer. If a background virus scanner randomly decides it's a good time to scan a text file for a virus and the computer freezes for a fraction of a second, there will be ugly gaps between the particles. For example, from the system in the above image, you might have periods of time that look something like this:

A better approach would be to store how much time has passed total, then create as many particles in that frame as needed to use up the time. Something like this:
timeAccum += timePassed;
while (timeAccum>0)
{
     CreateParticle();
     UpdateParticleMovementForJustCreatedParticle(timeAccum);
     timeAccum -= 1.0f/CREATION_FREQUENCY;
}
 (where timeAccum is the accumulated time left to process)
This will continuously emit particles regardless of how much time has passed. For example, lets say that you your trying to emit particles 5 times per second (0.2 second spacing). Things are going along nicely, but suddenly that evil virus scanner panics, and your game freezes for 0.5 seconds. So you have:
  initially: timeAccum=0.5
  after 1st pass: timeAccum = 0.3    1 particle that has moved 0.5 seconds of time
  after 2nd pass: timeAccum = 0.1    2 particles, one thats moved 0.5 seconds, the other 0.3 seconds
  after 3rd pass: timeAccum = -0.1    3 particles that have moved 0.5, 0.3, and 0.1 seconds of time
And with -0.1 left in timeAccum, another particle will be made in 0.1 seconds.


Particle Optimizations


For most particle systems to look good, you often need a lot of particles. This means keep the cost of each individual particle as low as reasonably possible. A good starting place is to use avoid allocating and freeing memory constantly. If you know the max number of particles you can have at any time, you could create an array of particles and flag each entry as active or inactive. Then to add a new particle, all that would be required is to mark an entry as active and set its data.

If your working in a 2D game thats got a semi-3D view, one very cheap way to get a 3D effect using 2D particles is to simply scale the y coordinate down (where y is vertical on the screen). This gives the illusion of an ortho projection in 3D. For a circular particle system, this can give you a "halo" type of effect. Though it looks better in motion, heres a simple example:

normal

    

y scaled

In many cases though, you're working in a 3D world with particles represented by simple 2D images that need to always be facing the viewer. For example, each particle might look like: . One common way to generate the vertices for these is by billboarding. This means doing a couple cross products at each particle to find two orthogonal directions that are orthogonal to a vector from the eye point to the particle. This is very similar to how many camera control schemes work. In pseudocode it will look something like:
VectorToViewer = Normalize(VIEWER-POS);
DirectionSide = CrossProduct(VectorToViewer, APPROXUP);
DirectionUp = CrossProduct(VectorToViewer, DirectionSide);
(where VIEWER is the 3d position of the camera, POS is the 3D position of the particle, and APPROXUP is the "approximate" up direction such as (0,0,1) )

The result of this, DirectionSide and DirectionUp, are two vectors that are perpendicular to each other and to the viewer. To get the vertices for the 4 corners of your particle, you would do something like:
Vertex0 = POS + DirectionUp*SIZE + DirectionSide*SIZE;
Vertex1 = POS + DirectionUp*SIZE - DirectionSide*SIZE;
Vertex2 = POS - DirectionUp*SIZE + DirectionSide*SIZE;
Vertex3 = POS - DirectionUp*SIZE - DirectionSide*SIZE;
 (where SIZE is the radius of the particle)

As you can imagine, doing this for every particle could be a little costly. If your rendering using the old fixed function pipeline, theres not a whole lot you can do. You can approximate the vectors for the entire system by replacing POS in the above code with the position of the center of the particle system, then use the resulting vectors for every particle. However if the particles are spread very far apart, or if the user is near the system, the outside particles begin to lose their shape. If the system is surrounding the viewer on several sides then this won't work at all. About the only optimization left in this case is to only recalculate those 2 directions every few frames (spread it evenly across the frames preferably, as opposed to doing all the calculations in a single frame).

However, if your using the programmable pipeline for your rendering, theres another very nice alternative using Vertex Shaders. Take a look at the following shader, written in HLSL:

float4x4 matViewProj; //combined view and projection transform
float4 cameraPos; //camera position in world space
float size; //particle size

//shader input
struct VS_INPUT
{
   float4 Pos : POSITION; //position in world space
   float2 Tex0 : TEXCOORD0;
};
//shader output
struct VS_OUTPUT
{
   float4 Pos : POSITION;
   float2 Tex0 : TEXCOORD0;
};

//shader code
VS_OUTPUT VShader(VS_INPUT In)
{
   VS_OUTPUT Out;

   //transform position and copy tex coord through
   Out.Pos=mul(matViewProj,In.Pos);
   Out.Tex0=In.Tex0;

   //expand outwards from center point, based on distance to viewer and tex coord
   float dist=distance(cameraPos,In.Pos);

   Out.Pos.xy+=(1.0f/sqrt(dist)) * (In.Tex0-0.5f) * size;

   //spit out the results
   return Out;
}

 All 4 input vertices of a particle would just have the same position (the center of the particle), with texture coordinates of (0,0) for upper left and (1,1) for lower right. At each vertex, the center point is transformed to screen space, then you stretch the corners outwards in 2D. The amount you pull them out is based on the distance from the particle to the camera, and the size of the particle. This is all done completely on the graphics hardware. Not only is the computation itself simpler (no cross products!), it means that the CPU has to do almost nothing for the rendering part.


Particle Demo


Here's a sample program I put together, that shows 2 different particle systems. These systems are the particle systems used in Sea of Chaos, with a few modifications. Both of these systems are fully 3D, drawn using only a simple still 2D image for each particle. They employ variations of the vertex shader technique mentioned above.

Fire:
This is the campfire in one of the screenshots above. Each particle rotates independently (a 2x2 transformation matrix is generated in the vertex shader). As the particles age, their rotation and speed slows down. They also grow as they get older, and their color shifts from yellow to red to transparent black. A wind force is also applied to each particle.

Water:
This is a fountain with water spewing from the top, and water dripping down from the top platter. It primarily demonstrates how a large number of particles is feasible even with seemingly complex behavior. Each particle can collide with either of the two platters of the fountain, or the ground plane. Upon collision, each particle breaks up into multiple other particles which in turn can collide again and break up further.

Requirements:
DirectX9.0c
A video card with hardware vertex shader support (VS1.1 or greater)
Reasonably fast processor is recommended

The W and F keys change between the demos. Escape exits.

Sea of Chaos Particle Demo


(c)2012 Luke Lenhart   -  97445 total visitors